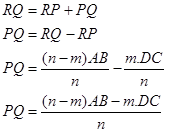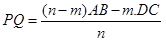Kamis, 28 November 2013
Karinding Karindingmangrupa salah sahiji alat musik tiup tradisional Sunda. Aya sababaraha wewengkon nu dipikawanoh minangka wewengkon nu ngahasilkeun karinding, nyaeta: Citamiang, Pasirmukti, Tasikmalaya,Lewo Malangbong, ( Garut),jeung Cikalongkulon ( Cianjur) nu nyieun karinding tina palapah kawung(enau). Di wewengkon Limbangan jeung Cililin mah, karinding teh dijieunna tina awi, ieu nandaan taun dijieunna, jeung nu makena ge para wanoja istri, hal ieu katiten tina wangunna nu jiga cucuk gelung nu gampil ditancebkeun dina gelung para wanoja rambut. karinding tina kawung lolobana dipake ku lalaki, wangunna leuwih pondok ngarah bisa diselapkeun dina wadah bako. Wangun karinding aya tilu buku (ruas). Sumber : http://su.m.wikipedia.org/wiki/Karinding
Senin, 25 November 2013
Selasa, 06 November 2012
Rumus Kesebangunan
Rumus Kesebangunan (Tugas)
Rumus Kesebangunan
Dua bangun dikatakan sebangun jika
a. panjang sisi-sisi yang bersesuaian dari kedua bangun tersebut memiliki perbandingan senilai
b. sudut-sudut yang bersesuaian dari kedua bangun tersebut sama besar.
2. Bangun-bangun yang memiliki bentuk dan ukuran yang sama dikatakan bangun-bangun yang kongruen.
3. Syarat dua segitiga sebangun adalah sisi-sisi yang bersesuaian sebanding atau sudut-sudut yang bersesuaian sama besar.
4. Syarat dua segitiga kongruen:
a. Sisi-sisi yang bersesuaian sama panjang (s.s.s)
b. Dua sisi yang bersesuaian sama panjang dan sudut yang diapitnya sama besar (s.sd.s)
c. Dua sudut yang bersesuaian sama besar dan sisi yang berada di antaranya sama panjang (sd.s.sd)
d. Dua sudut yang bersesuaian sama besar dan sisi yang berada di hadapannya sama panjang (sd.sd.s).
Yang pertama : untuk kasus siku-siku
Yang kedua : untuk segitiga sembarang
Penurunan rumus kesebangunan
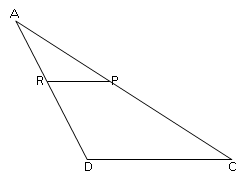
Berapa panjang PQ jika AB (sisi yang panjang) dan DC (sisi yang pendek) diketahui panjangnya dan perbandingan AP : AC = BQ : BD diketahui.
Pada posting sebelumnya, House of Math sudah mengulas cara menyelesaikan soal tersebut. Namun cara yang digunakan lumayan panjang. Nah sekarang House of Math akan mengulas tentang rumus cepat untuk menyelesaikan soal tersebut.
Dengan menggunakan proses berfikir pada posting pembahasan soal tersebut, kita bisa menurunkan rumus cepatnya. Inilah caranya:
1. Kita buat perpanjangan garis PQ di R
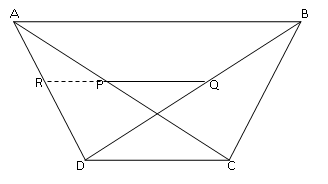
2. Misal = AP : AC = BQ : BD = m : n
3. Selanjutnya Pandang segitiga ADC
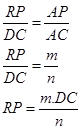
4. Pandang segitiga ABD
Berlaku hubungan:
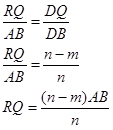
5. RQ merupakan sebuah garis yang dapat dibentuk olah garis RP dan garis RQ sehingga:
6. Sehingga untuk menghitung panjang PQ dapat langsung menggunakan rumus :
Dengan:
AB = sisi yang panjang
DC = sisi yang pendek
m : n = perbandingan letak P dan Q (kecil : besar)
Sekian penurunan rumus cepatnya, sepanjang itu menghasilkan rumus yang singkat,yang cepat, yang memudahkan pengerjaan soal.
Peluang
Peluang, Permutasi & Kombinasi Matematika
1) Permutasi
Permutasi adalah susunan unsur-unsur yang berbeda dalam urutan tertentu. Pada permutasi urutan diperhatikan sehingga
Permutasi k unsur dari n unsur
adalah
semua urutan yang berbeda yang mungkin dari k unsur yang diambil dari n
unsur yang berbeda. Banyak permutasi k unsur dari n unsur ditulis 
atau 
.Permutasi siklis (melingkar) dari n unsur adalah (n-1) !
Cara cepat mengerjakan soal permutasi
dengan penulisan nPk, hitung 10P4Contoh permutasi siklis :
kita langsung tulis 4 angka dari 10 mundur, yaitu 10.9.8.7
jadi 10P4 = 10x9x8x7 berapa itu? hitung sendiri
Suatu keluarga yang terdiri atas 6 orang duduk mengelilingi sebuah meja makan yang berbentuk lingkaran. Berapa banyak cara agar mereka dapat duduk mengelilingi meja makan dengan cara yang berbeda?
Jawab :
Banyaknya cara agar 6 orang dapat duduk mengelilingi meja makan dengan urutan yang berbeda sama dengan banyak permutasi siklis (melingkar) 6 unsur yaitu :
2) Kombinasi
Kombinasi adalah susunan unsur-unsur dengan tidak memperhatikan urutannya. Pada kombinasi AB = BA. Dari suatu himpunan dengan n unsur dapat disusun himpunan bagiannya dengan untuk
Setiap himpunan bagian dengan k unsur dari himpunan dengan unsur n disebut kombinasi k unsur dari n yang dilambangkan dengan , 
Contoh :
Diketahui himpunan
.Tentukan banyak himpunan bagian dari himpunan A yang memiliki 2 unsur!
Jawab :
Banyak himpunan bagian dari A yang memiliki 2 unsur adalah C (6, 2).
Cara cepat mengerjakan soal kombinasi
dengan penulisan nCk, hitung 10C4kita langsung tulis 4 angka dari 10 mundur lalu dibagi 4!, yaitu 10.9.8.7 dibagi 4.3.2.1
jadi 10C4 = 10x9x8x7 / 4x3x2x1 berapa itu? hitung sendiri
Ohya jika ditanya 10C6 maka sama dengan 10C4, ingat 10C6=10C4. contoh lainnya
20C5=20C15
3C2=3C1
100C97=100C3
melihat polanya? hehe semoga bermanfaat!
Peluang Matematika
1. Pengertian Ruang Sampel dan Kejadian Himpunan S dari semua kejadian atau peristiwa yang mungkin mucul dari suatu percobaan disebut ruang sampel. Kejadian khusus atau suatu unsur dari S disebut titik sampel atau sampel. Suatu kejadian A adalah suatu himpunan bagian dari ruang sampel S.
Contoh:2. Pengertian Peluang Suatu Kejadian
Diberikan percobaan pelemparan 3 mata uang logam sekaligus 1 kali, yang masing-masing memiliki sisi angka ( A ) dan gambar ( G ). Jika P adalah kejadian muncul dua angka, tentukan S, P (kejadian)!
Jawab :
S = { AAA, AAG, AGA, GAA, GAG, AGG, GGA, GGG}
P = {AAG, AGA, GAA}
Pada suatu percobaan terdapat n hasil yang mungkin dan masing-masing berkesempatan sama untuk muncul. Jika dari hasil percobaan ini terdapat k hasil yang merupakan kejadian A, maka peluang kejadian A ditulis P ( A ) ditentukan dengan rumus :
Contoh :
Pada percobaan pelemparan sebuah dadu, tentukanlah peluang percobaan kejadian muncul bilangan genap!
Jawab : S = { 1, 2, 3, 4, 5, 6} maka n ( S ) = 6
Misalkan A adalah kejadian muncul bilangan genap, maka:
A = {2, 4, 6} dan n ( A ) = 3
3. Kisaran Nilai Peluang Matematika
Misalkan A adalah sebarang kejadian pada ruang sampel S dengan n ( S ) = n, n ( A ) = k dan
Jadi, peluang suatu kejadian terletak pada interval tertutup [0,1]. Suatu kejadian yang peluangnya nol dinamakan kejadian mustahil dan kejadian yang peluangnya 1 dinamakan kejadian pasti.
4. Frekuensi Harapan Suatu Kejadian
Jika A adalah suatu kejadian pada frekuensi ruang sampel S dengan peluang P ( A ), maka frekuensi harapan kejadian A dari n kali percobaan adalah n x P( A ).
Contoh :Frekuensi harapan munculnya mata dadu 1 adalah
Bila sebuah dadu dilempar 720 kali, berapakah frekuensi harapan dari munculnya mata dadu 1? Jawab :
Pada pelemparan dadu 1 kali, S = { 1, 2, 3, 4, 5, 6 } maka n (S) = 6.
Misalkan A adalah kejadian munculnya mata dadu 1, maka:
A = { 1 } dan n ( A ) sehingga :
5. Peluang Komplemen Suatu Kejadian
Misalkan S adalah ruang sampel dengan n ( S ) = n, A adalah kejadian pada ruang sampel S, dengan n ( A ) = k dan Ac adalah komplemen kejadian A, maka nilai n (Ac) = n – k, sehingga :
Jadi, jika peluang hasil dari suatu percobaan adalah P, maka peluang hasil itu tidak terjadi adalah (1 – P).
Peluang Kejadian Majemuk
1. Gabungan Dua Kejadian Untuk setiap kejadian A dan B berlaku :
Catatan :
dibaca “ Kejadian A atau B dan 
dibaca “Kejadian A dan B”Contoh :
Pada pelemparan sebuah dadu, A adalah kejadian munculnya bilangan komposit dan B adalah kejadian muncul bilangan genap. Carilah peluang kejadian A atau B!
Jawab :
2. Kejadian-kejadian Saling Lepas
Untuk setiap kejadian berlaku
Jika 
. Sehingga 
Dalam kasus ini, A dan B disebut dua kejadian saling lepas.3. Kejadian Bersyarat
Jika P (B) adalah peluang kejadian B, maka P (A|B) didefinisikan sebagai peluang kejadian A dengan syarat B telah terjadi. Jika
adalah peluang terjadinya A dan B, maka 
Dalam kasus ini, dua kejadian tersebut tidak saling bebas.4. Teorema Bayes
Teorema Bayes(1720 – 1763) mengemukakan hubungan antara P (A|B) dengan P ( B|A ) dalam teorema berikut ini :
5. Kejadian saling bebas Stokhastik
(i) Misalkan A dan B adalah kejadian – kejadian pada ruang sampel S, A dan B disebut dua kejadian saling bebas stokhastik apabila kemunculan salah satu tidak dipengaruhi kemunculan yang lainnya atau : P (A | B) = P (A), sehingga:
Sebaran Peluang
1. Pengertian Peubah acak dan Sebaran Peluang. Peubah acak X adalah fungsi dari suatu sampel S ke bilangan real R. Jika X adalah peubah acak pada ruang sampel S denga X (S) merupakan himpunan berhingga, peubah acak X dinamakan peubah acak diskrit. Jika Y adalah peubah acak pada ruang sampel S dengan Y(S) merupakan interval, peubah acak Y disebut peubah acak kontinu. Jika X adalah fungsi dari sampel S ke himpunan bilangan real R, untuk setiap
dan setiap 
maka:
Misalkan X adalah peubah acak diskrit pada ruang sampel S, fungsi masa peluang disingkat sebaran peluang dari X adalah fungsi f dari R yang ditentukan dengan rumus berikut :
2. Sebaran Binom
Sebaran Binom atau Distribusi Binomial dinyatakan dengan rumus sebagai berikut :
Dengan P sebagai parameter dan
Rumus ini dinyatakan sebagai:
untuk n = 0, 1, 2, …. Dengan P sebagai parameter dan
P = Peluang sukses
n = Banyak percobaan
x = Muncul sukses
n-x = Muncul gagalRumus Peluang. sumber : http://rumusmatematikasmp9.blogspot.com/
Unit Pemroses Sentral
Dari Wikipedia bahasa Indonesia, ensiklopedia bebas
Unit Pemroses Sentral (UPS) (bahasa Inggris: Central Processing Unit; CPU), merujuk kepada perangkat keras komputer yang memahami dan melaksanakan perintah dan data dari perangkat lunak. Istilah lain, pemroses/prosesor (processor), sering digunakan untuk menyebut CPU. Adapun mikroprosesor adalah CPU yang diproduksi dalam sirkuit terpadu, seringkali dalam sebuah paket sirkuit terpadu-tunggal. Sejak pertengahan tahun 1970-an, mikroprosesor sirkuit terpadu-tunggal ini telah umum digunakan dan menjadi aspek penting dalam penerapan CPU.
Daftar isi
Komponen CPU
- Unit kontrol yang mampu mengatur jalannya program. Komponen
ini sudah pasti terdapat dalam semua CPU. CPU bertugas mengontrol
komputer sehingga terjadi sinkronisasi kerja antarkomponen dalam
menjalankan fungsi-fungsi operasinya. termasuk dalam tanggung jawab unit
kontrol adalah mengambil intruksi-intruksi dari memori utama dan
menentukan jenis instruksi tersebut. Bila ada instruksi untuk
perhitungan aritmatika atau perbandingan logika, maka unit kendali akan
mengirim instruksi tersebut ke ALU. Hasil dari pengolahan data dibawa
oleh unit kendali ke memori utama lagi untuk disimpan, dan pada saatnya
akan disajikan ke alat output. Dengan demikian tugas dari unit kendali
ini adalah:
- Mengatur dan mengendalikan alat-alat masukan (input) dan keluaran (output).
- Mengambil instruksi-instruksi dari memori utama.
- Mengambil data dari memori utama (jika diperlukan) untuk diproses.
- Mengirim instruksi ke ALU bila ada perhitungan aritmatika atau perbandingan logika serta mengawasi kerja dari ALU.
- Menyimpan hasil proses ke memori utama.
- Register merupakan alat penyimpanan kecil yang mempunyai kecepatan akses cukup tinggi, yang digunakan untuk menyimpan data dan/atau instruksi yang sedang diproses. Memori ini bersifat sementara, biasanya digunakan untuk menyimpan data saat di olah ataupun data untuk pengolahan selanjutnya. Secara analogi, register ini dapat diibaratkan sebagai ingatan di otak bila kita melakukan pengolahan data secara manual, sehingga otak dapat diibaratkan sebagai CPU, yang berisi ingatan-ingatan, satuan kendali yang mengatur seluruh kegiatan tubuh dan mempunyai tempat untuk melakukan perhitungan dan perbandingan logika.
- ALU unit yang bertugas untuk melakukan operasi aritmetika dan operasi logika berdasar instruksi yang ditentukan. ALU sering di sebut mesin bahasa karena bagian ini ALU terdiri dari dua bagian, yaitu unit arithmetika dan unit logika boolean yang masing-masing memiliki spesifikasi tugas tersendiri. Tugas utama dari ALU adalah melakukan semua perhitungan aritmatika yang terjadi sesuai dengan instruksi program. ALU melakukan semua operasi aritmatika dengan dasar penjumlahan sehingga sirkuit elektronik yang digunakan disebut adder.
- CPU Interconnections adalah sistem koneksi dan bus yang menghubungkan komponen internal CPU, yaitu ALU, unit kontrol dan register-register dan juga dengan bus-bus eksternal CPU yang menghubungkan dengan sistem lainnya, seperti memori utama, piranti masukan /keluaran.
Cara Kerja CPU
Saat data dan/atau instruksi dimasukkan ke processing-devices, pertama sekali diletakkan di MAA (melalui Input-storage); apabila berbentuk instruksi ditampung oleh Control Unit di Program-storage, namun apabila berbentuk data ditampung di Working-storage). Jika register siap untuk menerima pengerjaan eksekusi, maka Control Unit akan mengambil instruksi dari Program-storage untuk ditampungkan ke Instruction Register, sedangkan alamat memori yang berisikan instruksi tersebut ditampung di Program Counter. Sedangkan data diambil oleh Control Unit dari Working-storage untuk ditampung di General-purpose register (dalam hal ini di Operand-register). Jika berdasar instruksi pengerjaan yang dilakukan adalah arithmatika dan logika, maka ALU akan mengambil alih operasi untuk mengerjakan berdasar instruksi yang ditetapkan. Hasilnya ditampung di Akumulator. Apabila hasil pengolahan telah selesai, maka Control Unit akan mengambil hasil pengolahan di Accumulator untuk ditampung kembali ke Working-storage. Jika pengerjaan keseluruhan telah selesai, maka Control Unit akan menjemput hasil pengolahan dari Working-storage untuk ditampung ke Output-storage. Lalu selanjutnya dari Output-storage, hasil pengolahan akan ditampilkan ke output-devices.Fungsi CPU
CPU berfungsi seperti kalkulator, hanya saja CPU jauh lebih kuat daya pemrosesannya. Fungsi utama dari CPU adalah melakukan operasi aritmatika dan logika terhadap data yang diambil dari memori atau dari informasi yang dimasukkan melalui beberapa perangkat keras, seperti papan tombol, pemindai, tuas kontrol, maupun tetikus. CPU dikontrol menggunakan sekumpulan instruksi perangkat lunak komputer. Perangkat lunak tersebut dapat dijalankan oleh CPU dengan membacanya dari media penyimpan, seperti cakram keras, disket, cakram padat, maupun pita perekam. Instruksi-instruksi tersebut kemudian disimpan terlebih dahulu pada memori fisik (MAA), yang mana setiap instruksi akan diberi alamat unik yang disebut alamat memori. Selanjutnya, CPU dapat mengakses data-data pada MAA dengan menentukan alamat data yang dikehendaki.Saat sebuah program dieksekusi, data mengalir dari RAM ke sebuah unit yang disebut dengan bus, yang menghubungkan antara CPU dengan MAA. Data kemudian didekode dengan menggunakan unit proses yang disebut sebagai pendekoder instruksi yang sanggup menerjemahkan instruksi. Data kemudian berjalan ke unit aritmatika dan logika (ALU) yang melakukan kalkulasi dan perbandingan. Data bisa jadi disimpan sementara oleh ALU dalam sebuah lokasi memori yang disebut dengan register supaya dapat diambil kembali dengan cepat untuk diolah. ALU dapat melakukan operasi-operasi tertentu, meliputi penjumlahan, perkalian, pengurangan, pengujian kondisi terhadap data dalam register, hingga mengirimkan hasil pemrosesannya kembali ke memori fisik, media penyimpan, atau register apabila akan mengolah hasil pemrosesan lagi. Selama proses ini terjadi, sebuah unit dalam CPU yang disebut dengan penghitung program akan memantau instruksi yang sukses dijalankan supaya instruksi tersebut dapat dieksekusi dengan urutan yang benar dan sesuai.
Percabangan instruksi
Pemrosesan instruksi dalam CPU dibagi atas dua tahap, Tahap-I disebut Instruction Fetch, sedangkan Tahap-II disebut Instruction Execute. Tahap-I berisikan pemrosesan CPU dimana Control Unit mengambil data dan/atau instruksi dari main-memory ke register, sedangkan Tahap-II berisikan pemrosesan CPU dimana Control Unit menghantarkan data dan/atau instruksi dari register ke main-memory untuk ditampung di MAA, setelah Instruction Fetch dilakukan. Waktu pada tahap-I ditambah dengan waktu pada tahap-II disebut waktu siklus mesin (machine cycles time).Penghitung program dalam CPU umumnya bergerak secara berurutan. Walaupun demikian, beberapa instruksi dalam CPU, yang disebut dengan instruksi lompatan, mengizinkan CPU mengakses instruksi yang terletak bukan pada urutannya. Hal ini disebut juga percabangan instruksi (branching instruction). Cabang-cabang instruksi tersebut dapat berupa cabang yang bersifat kondisional (memiliki syarat tertentu) atau non-kondisional. Sebuah cabang yang bersifat non-kondisional selalu berpindah ke sebuah instruksi baru yang berada di luar aliran instruksi, sementara sebuah cabang yang bersifat kondisional akan menguji terlebih dahulu hasil dari operasi sebelumnya untuk melihat apakah cabang instruksi tersebut akan dieksekusi atau tidak. Data yang diuji untuk percabangan instruksi disimpan pada lokasi yang disebut dengan flag.
Bilangan yang dapat ditangani
Kebanyakan CPU dapat menangani dua jenis bilangan, yaitu fixed-point dan floating-point. Bilangan fixed-point memiliki nilai digit spesifik pada salah satu titik desimalnya. Hal ini memang membatasi jangkauan nilai yang mungkin untuk angka-angka tersebut, tetapi hal ini justru dapat dihitung oleh CPU secara lebih cepat. Sementara itu, bilangan floating-point merupakan bilangan yang diekspresikan dalam notasi ilmiah, di mana sebuah angka direpresentasikan sebagai angka desimal yang dikalikan dengan pangkat 10 (seperti 3,14 x 1057). Notasi ilmiah seperti ini merupakan cara yang singkat untuk mengekspresikan bilangan yang sangat besar atau bilangan yang sangat kecil, dan juga mengizinkan jangkauan nilai yang sangat jauh sebelum dan sesudah titik desimalnya. Bilangan ini umumnya digunakan dalam merepresentasikan grafik dan kerja ilmiah, tetapi proses aritmatika terhadap bilangan floating-point jauh lebih rumit dan dapat diselesaikan dalam waktu yang lebih lama oleh CPU karena mungkin dapat menggunakan beberapa siklus detak CPU. Beberapa komputer menggunakan sebuah prosesor sendiri untuk menghitung bilangan floating-point yang disebut dengan FPU (disebut juga math co-processor) yang dapat bekerja secara paralel dengan CPU untuk mempercepat penghitungan bilangan floating-point. FPU saat ini menjadi standar dalam banyak komputer karena kebanyakan aplikasi saat ini banyak beroperasi menggunakan bilangan floating-point. sumber : http://id.wikipedia.org/wiki/Unit_Pemroses_Sentral
Langganan:
Postingan (Atom)